当前位置：首页 > 新闻资讯 > 行业新闻

音级越多越高级? 没有这回事.

某种程度上说音符是算出来的, 音级可以任意多

5个7个区别只在于迭代的次数不一样

往下算还能算出12个, 这是现在常用的十二平均律的原型

再往下算甚至可以有19个,53, 665个等等, 不过太多了没法玩了...

这个问题问的非常好, 从这个问题开始能讲清楚俩最基本的概念: 音级和音程声音说到底就是振动, 振动的速度可以用频率表示. 现代研究表明, 人耳的敏感程度与声音频率大致呈指数关系. 举个例子: 对人耳而言，220Hz 到440Hz之间的差距跟 440Hz 到 880Hz 之间相同。所以就给他们相同的音名比如A, 然后划分为不同的音域虽然古人不懂物理和生物, 但是他们还是不约而同依据经验发现了这个现象每当声音的频率翻倍, 那我们就记他为一个单位, 西方叫八度, 东方叫均

现代研究又表明, 同时发俩音的话, 波形越有规律越好听！

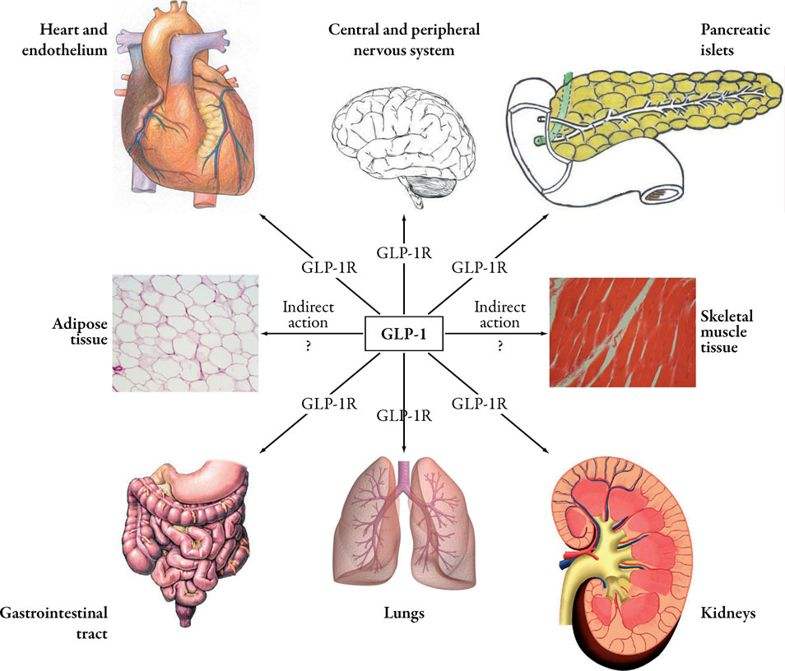
古人同样的, 成功发现了这个道理, 古人是不懂频率, 但是他们也可以听出音高不是...

可是他们发现了一个 2:3 很好听, 这个今天叫做纯五度.

好的, 可是只有两个音太单调了不是, 还能不能细分出更多的音呢?

于是就有了五度相生律, 每次升纯五度, 产生一个音, 因此得名

基准音频率设为 , 纯五度很好听, 也就是 和基准音 组合的时候很好听.

那么同样的道理 和 组合是不是也很好听啊?

但是注意这个超过两倍了, 前面说了一个八度两倍频率, 这里超了.

那怎么办呢? 还记得频率二倍感觉相似吗? 那除二不就行了?

所以第三个音符算出来应该是 , 以此类推, 算n次的音符是

我们取前7个, 排个序, 给他7个编号就行, 按现在的记法, 习惯基准音选为C, 那就是 CDEFGAB.

还没完啊, 凭什么算7次, 不多算也不少算?

你是可以随便算几次.

但你每次频率按这个倍增至少要能回去不是?

如果取5个音乘起来, 听起来和倍增3次相似, 压回去听起来还行.

取六个音, 你准备怎么压, 你说压三次还是四次好....

同理如果是7个音近似的压4次就好, 12 个音乐, 压7次就好...

这是2000年前古希腊的毕达哥斯拉学派的成就.

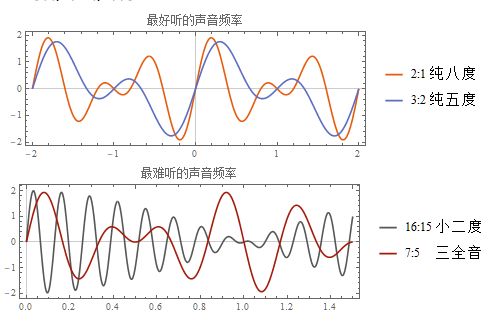
下一次两个指数偶遇要到41, 41 其实不怎么好, 再下一次是 , 程序员一眼就能看出后面是多少次方了>>逃...

2000年前西汉学者京房算出了这个...可是显然没人用的啊...

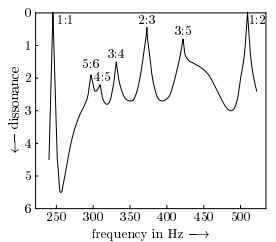
再下一次...停, 这个涉及丢番图逼近, 再说变成数学课了, 难道现在还不够像数学课吗>>逃

其实很简单的, 就是求 的线性逼近, 解由连分展开式所表达.